What mat statistics. Introduction to Mathematical Statistics

Mathematical statistics is a branch of mathematics devoted to mathematical methods of systematization, processing and use of statistical data for scientific and practical purposes.

Statistical data is information about the number and nature of objects in any more or less extensive collection that have certain properties.

A research method based on the consideration of statistical data from certain sets of objects is called statistical.

The formal mathematical side of statistical research methods is indifferent to the nature of the objects under study and constitutes the subject of mathematical statistics.

The main task of mathematical statistics is to obtain conclusions about mass phenomena and processes based on observations of them or experiments.

Statistics is a science that allows us to see patterns in the chaos of random data, highlight established connections in them and determine our actions in order to increase the proportion of correctly made decisions.

Many now known relationships between various aspects of the world around us were obtained by analyzing the data accumulated by humanity. After statistical detection of dependencies, a person already finds one or another rational explanation for the discovered patterns.

To outline the initial definitions of statistics, let's look at an example.

Example. Suppose it is necessary to estimate the degree of change in the IQ of 100 students over 3 years of study. As an indicator, consider the ratio of the current coefficient to the previously measured coefficient (three years ago), multiplied by 100%.

Let's get a sequence of 100 random variables: 97.8; 97.0; 101.7; 132.5; 142; ...; 122. Let us denote it by X.

Definition 1. The sequence of random variables X observed as a result of a study is called a sign in statistics.

Definition 2.Various meanings characteristics are called variants.

From the given values, it is difficult to obtain some information about the dynamics of changes in the IQ during the learning process. Let's arrange this sequence in ascending order: 94; 97.0; 97.8; …142. From the resulting sequence it is already possible to extract some useful information– for example, it is easy to determine the minimum and maximum value sign. But it is not clear how the characteristic is distributed among the entire population of students surveyed. Let's divide the options into intervals. According to the Sturges formula, the recommended number of intervals

m= 1+3.32l g(n)≈ 7.6, and the value of the interval is .

The ranges of the obtained intervals are given in column 1 of the table.

Let's count how many characteristic values ​​fall into each interval and write them in column 3.

Definition 3.A number showing how many options are included in a given i-th interval, is called frequency and is denoted by n i.

Definition 4.The ratio of frequency to the total number of observations is called relative frequency (wi) or weight.

Definition 5.A variation series is a series of options arranged in ascending or descending order with their corresponding weights.

For this example the options are the middles of the intervals.

Definition 6.Cumulative frequency( )a number variant with a characteristic value less than x (хОR) is called.

“Some people think they are always right. Such people could neither be good scientists nor have any interest in statistics... The case was brought down from heaven to earth, where it became part of the world of science.” (Diamand S.)

“Chance is only the measure of our ignorance. Random phenomena, if we define them, will be those whose laws we do not know.” (A. Poincaré “Science and Hypothesis”)

“Thank goodness. Isn't it the case
Always on par with the immutable...
Chance often rules the event,
Generates both joy and pain.
And life sets a task before us:
How to comprehend the role of chance"
(from the book “Mathematics studies randomness” by B.A. Kordemsky)

The world itself is natural - this is how we often consider and study the laws of physics, chemistry, etc., and yet nothing happens without the intervention of chance, which arises under the influence of unstable, side causal relationships that change the course of a phenomenon or experience when it is repeated. A “random effect” is created with the inherent regularity of “hidden predetermination”, i.e. chance has a need for a natural outcome.

Mathematicians consider random events only in the dilemma “to be or not to be” - whether it will happen or not.

Definition. The branch of applied mathematics in which the quantitative characteristics of mass random events or phenomena are studied is called mathematical statistics.

Definition. The combination of elements of probability theory and mathematical statistics is called stochastics.

Definition. Stochastics- this is the branch of mathematics that arose and is developing in close connection with the practical activities of man. Today, elements of stochastics are included in mathematics for everyone and are becoming a new, important aspect of mathematical and general education.

Definition. Mathematical statistics– the science of mathematical methods of systematization, processing and use of statistical data for scientific and practical conclusions.

Let's talk about this in more detail.

The generally accepted point of view now is that mathematical statistics is the science of general ways processing the experimental results. In solving these problems, what must an experiment have in order for the judgments made on its basis to be correct? Mathematical statistics becomes, in part, the science of experimental design.

The meaning of the word “statistics” has undergone significant changes over the past two centuries, write famous modern scientists Hodges and Lehman, “the word “statistics” has the same root as the word “state” (state) and originally meant the art and science of management: the first teachers of statistics in universities 18th century Germany would today be called specialists in social sciences. Because government decisions are to some extent based on data about population, industry, etc. statisticians, naturally, began to be interested in such data, and gradually the word “statistics” began to mean the collection of data about the population, about the state, and then the collection and processing of data in general. There is no point in extracting data unless something useful comes from it, and statisticians naturally become involved in interpreting the data.

The modern statistician studies methods by which inferences can be made about a population from data typically obtained from a sample of the “population.”

Definition. Statistician– a person who deals with the science of mathematical methods of systematization, processing and use of statistical data for scientific and practical conclusions.

Mathematical statistics arose in the 17th century and developed in parallel with probability theory. The further development of mathematical statistics (second half of the 19th and early 20th centuries) is due, first of all, to P.L. Chebyshev, A.A. Markov, A.M. Lyapunov, K. Gauss, A. Quetelet, F. Galton, K. Pearson, and others. In the 20th, the most significant contribution to mathematical statistics was made by A.N. Kolmogorov, V.I. Romanovsky, E.E. Slutsky, N.V. Smirnov, B.V. Gnedenko, as well as the English Student, R. Fisher, E. Purson and American scientists (Y. Neumann, A. Wald).

Problems of mathematical statistics and the meaning of error in the world of science

The establishment of patterns to which mass random phenomena are subject is based on the study of statistical data from observational results using the methods of probability theory.

The first task of mathematical statistics is to indicate ways of collecting and grouping statistical information obtained as a result of observations or as a result of specially designed experiments.

The second task of mathematical statistics is to develop methods for analyzing statistical data depending on the objectives of the study.

Modern mathematical statistics is developing methods for determining the number of necessary tests before the start of a study (experiment planning) and during the study (sequential analysis). It can be defined as the science of decision making under uncertainty.

Briefly, we can say that the task of mathematical statistics is to create methods for collecting and processing statistical data.

When studying a mass random phenomenon, it is assumed that all tests are carried out under the same conditions, i.e. a group of main factors that can be taken into account (measurable) and have a significant impact on the test result retains the same values ​​as possible.

Random factors distort the result that would have been obtained if only the main factors were present, making it random. The deviation of the result of each test from the true one is called observation error, which is a random variable. It is necessary to distinguish between systematic and random errors.

A scientific experiment is as unthinkable without error as an ocean without salt. Any flow of facts that adds to our knowledge brings some kind of error. According to a well-known saying, in life most people cannot be sure of anything except death and taxes, and the scientist adds: “And the errors of experience.”

A statistician is a “bloodhound” who hunts for errors. Statistics tool for error detection.

The word “error” does not mean a simple “miscalculation”. The consequences of a miscalculation are a small and relatively uninteresting source of experimental error.

Indeed, our instruments break; our eyes and ears can deceive us; our measurements are never completely accurate, sometimes even our arithmetic calculations are erroneous. An experimental error is something more significant than an inaccurate tape measure or an optical illusion. And since the most important job of statistics is to help scientists analyze the error of an experiment, we must try to understand what an error really is.

Whatever problem a scientist works on, it will certainly turn out to be more complex than he would like. Let's say he measures radioactive fallout at different latitudes. Results will depend on the altitude of where samples are collected, the amount of local rainfall and the altitude of cyclones over a wider area.

Experimental error is an integral part of any truly scientific experiment.

The same result can be error and information depending on the problem and point of view. If a biologist wishes to investigate how changes in nutrition affect growth, then the presence of a related constitution is a source of error; if he studies the relationship between heredity and growth, the source of error will be differences in nutrition. If a physicist wants to study the relationship between electrical conductivity and temperature, differences in the density of the conducting material are a source of error; if he studies the relationship between this density and electrical conductivity, temperature changes will be a source of error.

This use of the word error may seem dubious, and it might be preferable to say that the effects obtained are confounded by “unintended” or “undesirable” influences. We design an experiment to study known influences, but random factors that we cannot predict or analyze skew the results by adding their own effects.

The difference between planned effects and effects due to random causes is like the difference between the movements of a ship at sea, sailing along a certain course, and a ship drifting aimlessly under the will of changing winds and currents. The movement of the second vessel can be called random movement. It is possible that this ship may arrive at some port, but it is more likely that it will not arrive at any specific place.

Statisticians use the word “random” to denote a phenomenon whose outcome at the next moment in time is completely impossible to predict.

The error caused by the effects foreseen in the experiment is sometimes more systematic than random.

Systematic error is more misleading than random error. Interference coming from another radio station can create a systematic musical accompaniment that you can sometimes predict if you know the tune. But this “accompaniment” may be the reason why we may make an incorrect judgment about the words or the music of the program we are trying to hear.

However, the discovery of a systematic error often leads us to the trail of a new discovery. Knowing how random errors occur helps us detect systematic errors and therefore eliminate them.

The same nature of reasoning is common in our everyday affairs. How often do we notice: “This is not an accident!” Whenever we can say this, we are on the path to discovery.

For example, A.L. Chizhevsky, analyzing historical processes: increased mortality, epidemics, outbreaks of wars, great movements of peoples, sudden climate changes, etc. discovered the relationship between these unrelated processes and periods of solar activity, which have cycles: 11 years, 33 years.

Definition. Under systematic error is understood as an error that is repeated and the same for all tests. It is usually associated with improper conduct of the experiment.

Definition. Under random mistakes refers to errors that arise under the influence of random factors and vary randomly from experiment to experiment.

Typically, the distribution of random errors is symmetrical about zero, from which an important conclusion follows: in the absence of systematic errors, the true test result is the mathematical expectation of a random variable, the specific value of which is fixed in each test.

The objects of study in mathematical statistics can be qualitative or quantitative characteristics of the phenomenon or process being studied.

In the case of a qualitative feature, the number of occurrences of this feature in the considered series of experiments is counted; this number represents the (discrete) random variable being studied. Examples of quality attributes include defects on a finished part, demographic data, etc. If the characteristic is quantitative, then in the experiment direct or indirect measurements are made by comparison with some standard - a unit of measurement - using various measuring instruments. For example, if there is a batch of parts, then the standard of the part can serve as a qualitative sign, and the controlled size of the part can serve as a quantitative sign.

Basic definitions

A significant part of mathematical statistics is associated with the need to describe a large collection of objects.

Definition. The entire set of objects to be studied is called the general population.

The general population can be the entire population of the country, the monthly production of a plant, the population of fish living in a given reservoir, etc.

But the population is not just a set. If the set of objects we are interested in is too numerous, or the objects are difficult to access, or there are other reasons that do not allow us to study all the objects, we resort to studying some part of the objects.

Definition. That part of the objects that was subject to inspection, research, etc. is called sample population or just sampling.

Definition. The number of elements in the population and sample is called their volumes.

How to ensure that the sample best represents the whole, i.e. would it be representative?

If the whole, i.e. if the population is little or completely unknown to us, we cannot offer anything better than a purely random selection. Greater awareness allows you to act better, but still, at some stage, ignorance sets in and, as a result, random choice.

But how to make a purely random choice? As a rule, selection occurs according to easily observable characteristics, for the sake of which research is conducted.

Violation of the principles of random selection led to serious errors. A poll conducted by the American magazine Literary Review regarding the outcome of the presidential election in 1936 became famous for its failure. The candidates in this election were F.D. Roosevelt and A.M. Landon.

Who won?

The editors used telephone books as a general population. After randomly selecting 4 million addresses, she sent postcards asking about attitudes toward presidential candidates across the country. After spending a large sum on mailings and postcard processing, the magazine announced that Landon would win the upcoming presidential election by a landslide. The election result was the opposite of this forecast.

Two mistakes were made here at once. First, phone books do not provide a representative sample of the US population—mostly wealthy heads of household. Secondly, not all people sent answers, but largely from representatives of the business world, who supported Landon.

At the same time, sociologists J. Gallan and E. Warner correctly predicted the victory of F.D. Roosevelt, based only on four thousand questionnaires. The reason for this success was not only the correct sampling. They took into account that society is divided into social groups that are more homogeneous in relation to presidential candidates. Therefore, the sample from the layer can be relatively small with the same accuracy result. In the end, Roosevelt, who was a supporter of reforms for the less wealthy sections of the population, won.

Having the results of the survey by strata, it is possible to characterize society as a whole.

What are samples?

These are series of numbers.

Let us dwell in more detail on the basic concepts that characterize the sample series.

A sample of size n was extracted from the general population > n 1, where n 1 is the number of times the appearance of x 1, n 2 - x 2, etc. was observed.

The observed values ​​of x i are called variants, and the sequence of variants written in ascending order is called a variation series. The numbers of observations n i are called frequencies and n i /n - relative frequencies (or frequencies).

Definition. Different values ​​of a random variable are called options.

Definition. Variation series is a series arranged in ascending (or descending) order of options with their corresponding frequencies (frequencies).

When studying variation series, along with the concepts of frequency, the concept of accumulated frequency is used. The accumulated frequencies (frequencies) for each interval are found by sequentially summing the frequencies of all previous intervals.

Definition. The accumulation of frequencies or frequencies is called cumulation. You can cumulate frequencies and intervals.

The characteristics of a series can be quantitative and qualitative.

Quantitative (variational) characteristics- These are characteristics that can be expressed in numbers. They are divided into discrete and continuous.

Qualitative (attributive) characteristics– these are characteristics that are not expressed in numbers.

Continuous Variables are variables that are expressed as real numbers.

Discrete Variables are variables that can only be expressed as integers.

The samples are characterized central tendencies: mean, mode and median. The average value of a sample is the arithmetic mean of all its values. The sampling mode is those values ​​that occur most often. The sample median is the number that “splits” in half the ordered population of all values ​​in the sample.

The variation series can be discrete or continuous.

Task

Sample given: 1.3; 1.8; 1.2; 3.0; 2.1; 5; 2.4; 1.2; 3.2;1.2; 4; 2.4.

This is a range of options. Arranging these options in ascending order, we get a variation series: 1.2; 1.2; 1.2; 1.3; 1.8; 2.1; 2.4; 2.4; 3.0; 3.2; 4; 5.

The average value of this series is 2.4.

The median of the series is 2.25.

The mode of the series is –1,2.

Let us define these concepts.

Definition. Median of the variation series The value of the random variable that falls in the middle of the variation series (Me) is called.

The median of an ordered series of numbers with an odd number of terms is the number written in the middle, and the median of an ordered series of numbers with an even number of terms is the arithmetic mean of the two numbers written in the middle. The median of an arbitrary series of numbers is the median of the corresponding ordered series.

Definition. Variation series fashion They call the option (the value of the random variable) to which the highest frequency (Mo) corresponds, i.e. which occurs more often than others.

Definition. The arithmetic mean value of the variation series is the result of dividing the sum of the values ​​of a statistical variable by the number of these values, that is, by the number of terms.

The rule for finding the arithmetic mean of a sample:

1. multiply each option by its frequency (multiplicity);
2. add up all the resulting products;
3. divide the found sum by the sum of all frequencies.

Definition. Row range is called the difference between R=x max -x min, i.e. the largest and smallest values ​​of these options.

Let's check whether we correctly found the mean value of this series, median and mode, based on the definitions.

We counted the number of terms, there are 12 of them - an even number of terms, which means we need to find the arithmetic mean of the two numbers written in the middle, that is, the 6th and 7th options. (2.1+2.4)\2=2.25 – median.

Fashion. The fashion is 1.2, because only this number occurs 3 times, and the rest occur less than 3 times.

We find the arithmetic mean like this:

(1,2*3+1,3+1,8+2,1+2,4*2+3,0+3,2 +4+5)\12=2,4

Let's make a table

Such tables are called frequency tables. In them, the numbers in the second line are frequencies; they show how often certain values ​​occur in the sample.

Definition. Relative frequency sample values ​​is the ratio of its frequency to the number of all sample values.

Relative frequencies are otherwise called frequencies. Frequencies and frequencies are called scales. Let's find the range of the series: R=5-1.2=3.8; The range of the series is 3.8.

Food for thought

The arithmetic mean is a conventional value. In reality it doesn't exist. In reality there is a total amount. Therefore, the arithmetic mean is not a characteristic of one observation; it characterizes the series as a whole.

Average value can be interpreted as the center of dispersion of the values ​​of the observed characteristic, i.e. value around which all observed values ​​fluctuate, and the algebraic sum of deviations from the average is always zero, i.e. the sum of deviations from the average upward or downward are equal.

Arithmetic mean is an abstract (generalizing) quantity. Even when specifying a series of only natural numbers, the average value can be expressed as a fraction. Example: GPA test work 3,81.

Average value is found not only for homogeneous quantities. Average grain yield throughout the country (corn - 50-60 centners per hectare and buckwheat - 5-6 centners per hectare, rye, wheat, etc.), average food consumption, average national income per capita , average housing supply, weighted average housing cost, average labor intensity of building construction, etc. - these are the characteristics of the state as a single national economic system, these are the so-called system averages.

In statistics, such characteristics as mode and median. They are called structural averages, because the values ​​of these characteristics are determined by the general structure of the data series.

Sometimes a series may have two modes, sometimes a series may have no mode.

Fashion is the most acceptable indicator when identifying the packaging of a certain product, which is preferred by buyers; prices for goods of a given type, common on the market; as the size of shoes, clothes, which is in greatest demand; a sport that the majority of the population of a country, city, village, school, etc. prefer to engage in.

In construction, there are 8 options for slabs in width, and 3 types are more often used: 1 m, 1.2 m and 1.5 m. In length, there are 33 options for slabs, but slabs with a length of 4.8 m are most often used; 5.7 m and 6.0 m, the slab fashion is most often found among these 3 sizes. The same can be said about window brands.

The mode of a data series is found when one wants to identify some typical indicator.

A mode can be expressed in numbers and words; from a statistical point of view, a mode is an extremum of frequency.

Median allows you to take into account information about a series of data that is given by the arithmetic mean and vice versa.

RANDOM VARIABLES AND THE LAWS OF THEIR DISTRIBUTION.

Random They call a quantity that takes values ​​depending on a combination of random circumstances. Distinguish discrete and random continuous quantities.

Discrete A quantity is called if it takes on a countable set of values. ( Example: the number of patients at a doctor's appointment, the number of letters on a page, the number of molecules in a given volume).

Continuous is a quantity that can take values ​​within a certain interval. ( Example: air temperature, body weight, human height, etc.)

Law of distribution random variable is called a population possible values this value and the probabilities (or frequencies of occurrence) corresponding to these values.

EXAMPLE:

x	x 1	x 2	x 3	x 4	...	x n
p	p 1	p 2	p 3	p 4	...	p n

x	x 1	x 2	x 3	x 4	...	x n
m	m 1	m 2	m 3	m 4	...	m n

NUMERICAL CHARACTERISTICS OF RANDOM VARIABLES.

In many cases, along with the distribution of a random variable or instead of it, information about these quantities can be provided by numerical parameters called numerical characteristics of a random variable . The most common of them:

1 .Expectation - (average value) of a random variable is the sum of the products of all its possible values ​​and the probabilities of these values:

2 .Dispersion random variable:

3 .Standard deviation :

“THREE SIGMA” rule - if a random variable is distributed according to a normal law, then the deviation of this value from the average value in absolute value does not exceed three times the standard deviation

GAUSS LAW – NORMAL DISTRIBUTION LAW

Often there are quantities distributed over normal law (Gauss's law). Main feature : it is the limiting law to which other laws of distribution approach.

A random variable is distributed according to the normal law if it probability density has the form:

M(X)- mathematical expectation of a random variable;

s- standard deviation.

Probability Density(distribution function) shows how the probability assigned to an interval changes dx random variable, depending on the value of the variable itself:

BASIC CONCEPTS OF MATHEMATICAL STATISTICS

Mathematical statistics- a branch of applied mathematics directly adjacent to probability theory. The main difference between mathematical statistics and probability theory is that mathematical statistics does not consider actions on distribution laws and numerical characteristics of random variables, but approximate methods for finding these laws and numerical characteristics based on the results of experiments.

Basic concepts mathematical statistics are:

1. General population;

2. sample;

3. variation series;

4. fashion;

5. median;

6. percentile,

7. frequency polygon,

8. histogram.

Population- a large statistical population from which part of the objects for research is selected

(Example: the entire population of the region, university students of a given city, etc.)

Sample (sample population)- a set of objects selected from the general population.

Variation series- statistical distribution consisting of variants (values ​​of a random variable) and their corresponding frequencies.

Example:

X,kg

m

x- value of a random variable (mass of girls aged 10 years);

m- frequency of occurrence.

Fashion– the value of the random variable that corresponds to the highest frequency of occurrence. (In the example above, the fashion corresponds to the value 24 kg, it is more common than others: m = 20).

Median– the value of a random variable that divides the distribution in half: half of the values ​​are located to the right of the median, half (no more) - to the left.

Example:

1, 1, 1, 1, 1. 1, 2, 2, 2, 3 , 3, 4, 4, 5, 5, 5, 5, 6, 6, 7 , 7, 7, 7, 7, 7, 8, 8, 8, 8, 8 , 8, 9, 9, 9, 10, 10, 10, 10, 10, 10

In the example we observe 40 values ​​of a random variable. All values ​​are arranged in ascending order, taking into account the frequency of their occurrence. You can see that to the right of the highlighted value 7 are 20 (half) of the 40 values. Therefore, 7 is the median.

To characterize the scatter, we will find the values ​​not higher than 25 and 75% of the measurement results. These values ​​are called 25th and 75th percentiles . If the median divides the distribution in half, then the 25th and 75th percentiles are cut off by a quarter. (The median itself, by the way, can be considered the 50th percentile.) As can be seen from the example, the 25th and 75th percentiles are equal to 3 and 8, respectively.

Use discrete (point) statistical distribution and continuous (interval) statistical distribution.

For clarity, statistical distributions are depicted graphically in the form frequency range or - histograms .

Frequency polygon- a broken line, the segments of which connect points with coordinates ( x 1 ,m 1), (x 2 ,m 2), ..., or for relative frequency polygon – with coordinates ( x 1,р * 1), (x 2 ,р ​​* 2), ...(Fig.1).

m m i /n f(x)

Fig.1 Fig.2

Frequency histogram- a set of adjacent rectangles built on one straight line (Fig. 2), the bases of the rectangles are the same and equal dx , and the heights are equal to the ratio of frequency to dx , or p* To dx (probability density).

Example:

x, kg	2,7	2,8	2,9	3,0	3,1	3,2	3,3	3,4	3,5	3,6	3,7	3,8	3,9	4,0	4,1	4,2	4,3	4,4
m

Frequency polygon

The ratio of relative frequency to interval width is called probability density f(x)=m i / n dx = p* i / dx

An example of constructing a histogram .

Let's use the data from the previous example.

1. Calculation of the number of class intervals

Where n - number of observations. In our case n = 100 . Hence:

2. Calculation of interval width dx :

,

3. Drawing up an interval series:

dx	2.7-2.9	2.9-3.1	3.1-3.3	3.3-3.5	3.5-3.7	3.7-3.9	3.9-4.1	4.1-4.3	4.3-4.5
m
f(x)	0.3	0.75	1.25	0.85	0.55	0.6	0.4	0.25	0.05

Histogram

Ministry of Education and Science of the Russian Federation

Kostroma State Technological University

I.V. Zemlyakova, O.B. Sadovskaya, A.V. Cherednikova

MATHEMATICAL STATISTICS

as a teaching aid for students of specialties

220301, 230104, 230201 full-time education

Kostroma

PUBLISHING HOUSE

UDC 519.22 (075)

Reviewers: department mathematical methods in economics
Kostromsky state university them. N.A. Nekrasova;

Ph.D. physics and mathematics Sciences, Associate Professor of the Department of Mathematical Analysis

Kostroma State University named after. N.A. Nekrasova K.E. Shiryaev.

Z 51 Zemlyakova, I.V. Mathematical statistics. Theory and practice: training manual/ I.V. Zemlyakova, O.B. Sadovskaya, A.V. Cherednikova. – Kostroma: Publishing house Kostroma. state technol. University, 2010. – 60 p.

ISBN 978-5-8285-0525-8

The textbook contains theoretical material, examples, tests and a commented algorithm for completing tasks based on standard calculations in the most accessible form.

Intended for university students studying full-time in specialties 220301, 230104, 230201. Can be used both during lectures and practical classes.

UDC 519.22 (075)

ISBN 978-5-8285-0525-8

 Kostroma State Technological University, 2010

§1. PROBLEMS OF MATHEMATICAL STATISTICS 4

§2. GENERAL AND SAMPLE POPULATION. 4

REPRESENTATIVENESS OF THE SAMPLE. SELECTION METHODS 4

(WAYS OF SAMPLING) 4

§3. STATISTICAL DISTRIBUTION OF THE SAMPLE. 6

GRAPHICAL REPRESENTATION OF DISTRIBUTIONS 6

§4. STATISTICAL ESTIMATES OF DISTRIBUTION PARAMETERS 18

§5. GENERAL AVERAGE. SAMPLE AVERAGE. 20

ASSESSMENT OF THE GENERAL AVERAGE BY THE SAMPLE AVERAGE 20

§6. GENERAL DISPERSION. SAMPLING VARIANCE. 22

ESTIMATION OF GENERAL VARIANCE BY CORRECTED VARIANCE 22

§7. METHOD OF MOMENTS AND METHOD OF MAXIMUM LIKELIHOOD FOR FINDING PARAMETER ESTIMATES. MOMENT METHOD 25

§8. CONFIDENCE PROBABILITY. CONFIDENCE INTERVAL 27

§9. CHECKING THE HYPOTHESIS ABOUT THE COMPLIANCE OF STATISTICAL DATA WITH THE THEORETICAL DISTRIBUTION LAW 31

§ 10. CONCEPT OF CORRELATION AND REGRESSIVE ANALYSIS 39

INDIVIDUAL TASKS 44

ANSWERS AND DIRECTIONS 46

Applications 51

§1. PROBLEMS OF MATHEMATICAL STATISTICS

The mathematical laws of probability theory are not abstract, devoid of physical content, they are a mathematical expression of real patterns that exist in mass random phenomena.

Every study of random phenomena carried out using methods of probability theory is based on experimental data.

The origin of mathematical statistics was associated with the collection of data and graphical presentation of the results obtained (summaries of fertility, marriages, etc.). This descriptive statistics. It was necessary to reduce extensive material to a small number of quantities. The development of methods for collecting (registration), describing and analyzing experimental (statistical) data obtained as a result of observing mass, random phenomena is subject of mathematical statistics.

In this case it is possible to highlight three stages:

data collection;

data processing;

statistical conclusions, forecasts and decisions.

Typical tasks mathematical statistics:

determination of the law of distribution of a random variable (or system of random variables) from statistical data;

testing the plausibility of hypotheses;

finding unknown distribution parameters.

So, task mathematical statistics consists of creating methods for collecting and processing statistical data to obtain scientific and practical conclusions.

§2. GENERAL AND SAMPLE POPULATION.

REPRESENTATIVENESS OF THE SAMPLE. SELECTION METHODS

(WAYS OF SAMPLING)

Mass random phenomena can be presented in the form of certain statistical collections of homogeneous objects. Each statistical population has different signs.

Distinguish quality And quantitative signs. Quantitative characteristics may vary continuously or discretely.

Example 1. Let's consider the production process (mass random phenomenon) of manufacturing a batch of parts (statistical population).

The standard nature of a part is a quality sign. The size of a part is a quantitative characteristic that changes continuously.

Let it be necessary to study a statistical set of homogeneous objects with respect to some characteristic. A continuous survey, i.e., a study of each of the objects of the statistical population, is rarely used in practice. If the study of an object is associated with its destruction or requires large material costs, then there is no point in conducting a complete survey. If a population contains a very large number of objects, then it is almost impossible to conduct a comprehensive survey. In such cases, a limited number of objects are randomly selected from the entire population and examined.

 Definition.General population is called the entire population to be studied.

 Definition.Sample population or sampling is a collection of randomly selected objects.

 Definition.Volume population (sample or general) is the number of objects in this population. The volume of the population is denoted by N, and samples through n.

In practice it is usually used non-repetitive sampling, in which the selected object is not returned to the general population (otherwise we get a repeat sample).

In order for sample data to be used to judge the entire population, the sample must be representative(representative). To do this, each object must be selected at random, and all objects must have the same probability of being included in the sample. apply various ways selection (Fig. 1).

Selection methods

(methods of organizing sampling)

Two stage

(the general population is divided

per group)

Single stage

(the general population is not divided

per group)

Simple random

(objects are retrieved randomly

from the whole set)

Typical

(object is selected from each typical part)

Combined

(from total number several groups are selected and from them several objects are selected)

Simple random resampling

random non-repetitive sampling

Mechanical

(from each group

select one object at a time)

Serial

(out of the total number of groups - series, several are selected

and they are thoroughly investigated)

Rice. 1. Selection methods

Example 2. The plant has 150 machines producing identical products.

1. Products from all 150 machines are mixed and several products are randomly selected - simple random sampling.

2. Products from each machine are arranged separately.

Several products are selected from all 150 machines, and products from more worn and less worn machines are analyzed separately - typical sample.

One product from each of the 150 machines - mechanical sample.

Out of 150 machines, several are selected (for example, 15 machines), and all products from these machines are examined - serial sample.

From 150 machines, several are selected, and then several products from these machines are selected - combined sample.

§3. STATISTICAL DISTRIBUTION OF THE SAMPLE.

GRAPHICAL REPRESENTATION OF DISTRIBUTIONS

Let it be necessary to study a statistical population with respect to some quantitative characteristic X. The numerical values ​​of the characteristic will be denoted by X i .

A sample size is extracted from the population p.

Quantitative characteristicX – discrete random variable.

Observed values X i called options, and the sequence of options written in ascending order is variation series.

Let x 1 observed n 1 once,

x 2 observed n 2 once,

x k observed n k once,

and
. Numbers n i called frequencies, and their relation to the sample size, i.e.
, – relative frequencies(or frequencies), and
.

The value of the option and the corresponding frequencies or relative frequencies can be written in the form of tables 1 and 2.

Table 1

Option x i	x 1	x 2		x k
Frequency n i	n 1	n 2		n k

Table 1 is called discretestatistical distribution series (DSD) of frequencies, or frequency table.

Table 2

Option x i	x 1	x 2		x k
Relative frequency w i	w 1	w 2		w k

Table 2 - DSR relative frequencies, or table of relative frequencies.

 Definition.Fashion the most common option is called, i.e. option with the highest frequency. Designated x Maud .

 Definition.Median This is the value of a characteristic that divides the entire statistical population, presented in the form of a variation series, into two equal parts. Designated
.

If n odd, i.e. n = 2 m + 1 , then = x m +1.

If n even, i.e. n = 2 m, That
.

Example 3 . Based on the results of observations: 1, 7, 7, 2, 3, 2, 5, 5, 4, 6, 3, 4, 3, 5, 6, 6, 5, 5, 4, 4, construct the DSR of relative frequencies. Find the mode and median.

Solution . Sample size n= 20. Let’s create a ranked series of sample elements: 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5, 6, 6, 6, 7, 7. Select options and count their frequencies (in brackets): 1 (1), 2 (2), 3 (3),
4 (4), 5 (5), 6 (3), 7 (2). We build the table:

x i
w i

Most common option x i = 5. Therefore, x Maud = 5. Since the sample size n is an even number, then

If we plot points on the plane and connect them with line segments, we get frequency range.

If we plot points on the plane, we get relative frequency polygon.

Example 4 . Construct a frequency polygon and a relative frequency polygon using the given sampling distribution:

x i

Within educational program At a university, you are unlikely to find a separate discipline called “mathematical statistics”; however, the elements of mathematical statistics are often studied in conjunction with probability theory, but only after studying the main course in probability theory.

Mathematical statistics: general information

Mathematical statistics is a branch of mathematics that develops methods for recording, describing and analyzing data from any observations and experiments, the purpose of which is to build probabilistic models of mass random phenomena.

Mathematical statistics as a science arose in the 17th century. and developed in parallel with probability theory. They made a great contribution to the development of science in the 19th-20th centuries. Chebyshev P.L., Gauss K., Kolmogorov A.N. etc.

The general task of mathematical statistics is to create methods for collecting and processing statistical data to obtain scientific and practical conclusions.

The main sections of mathematical statistics are:

• sampling method (familiarization with the concept of sampling, methods of collecting and processing data, etc.);
• statistical assessment of sample parameters (estimates, confidence intervals, etc.);
• calculation of summary characteristics of the sample (calculation of options, moments, etc.);
• correlation theory (regression equations, etc.);
• statistical testing of hypotheses;
• one-way analysis of variance.

TO most common Problems of mathematical statistics that are studied at university and often encountered in practice include:

• problems of determining estimates of sampling parameters;
• tasks to test statistical hypotheses;
• the problem of determining the type of distribution law based on statistical data.

Problems of determining sample parameter estimates

The study of mathematical statistics begins with the definition of such concepts as “sample”, “frequency”, “relative frequency”, “empirical function”, “polygon”, “cumulate”, “histogram”, etc. Next comes the study of the concepts of estimates (biased and unbiased): sample mean, variance, corrected variance, etc.

Task

Children's height measurement junior group kindergarten represented by a sample:
92, 96, 95, 96, 94, 97, 98, 94, 95, 96.
Let's find some characteristics of this sample.

Solution

Sample size (number of measurements; N): 10.
Lowest sample value: 92. Highest value samples: 98.
Sample range: 98 – 92 = 6.
Let's write down the ranked series (options in ascending order):
92, 94, 94, 95, 95, 96, 96, 96, 97, 98.
Let’s group the series and write it in a table (we’ll assign each option the number of its occurrences):

x i	92	94	95	96	97	98	N
n i	1	2	2	3	1	1	10

Let's calculate the relative frequencies and accumulated frequencies, write the result in the table:

x i	92	94	95	96	97	98	Total
n i	1	2	2	3	1	1	10
	0,1	0,2	0,2	0,3	0,1	0,1	1
Accumulated frequencies	1	3	5	8	1	10

Let's build a polygon of sampling frequencies (mark on the graph the options along the OX axis, frequencies along the OY axis, connect the points with a line).

We calculate the sample mean and variance using the formulas (respectively):

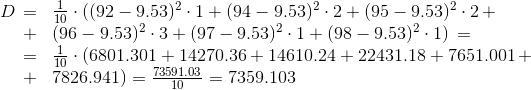
You can also find other characteristics of the sample, but for a general idea the characteristics found are sufficient.

Problems testing statistical hypotheses

Problems belonging to this type are more complex than problems of the previous type and their solution is often more voluminous and labor-intensive. Before starting to solve problems, the concepts of statistical hypothesis, null and competing hypothesis, etc. are first studied.

Let's consider simplest task of this type.

Task

Two independent samples of volume 11 and 14 are given, extracted from normal populations X, Y. Corrected variances are also known, equal to 0.75 and 0.4, respectively. It is necessary to test the null hypothesis about the equality of general variances at the significance level γ =0.05. Choose a competing hypothesis as desired.

Solution

The null hypothesis for our problem is written as follows:

As a competing hypothesis, consider the following:

Let us calculate the ratio of the larger corrected variance to the smaller one and obtain the observed value of the criterion:

Since the competing hypothesis we have chosen is of the form , the critical region is right-handed.
Using the table for a significance level of 0.05 and the numbers of degrees of freedom equal to 10 (11 – 1 = 10) and 13 (14 – 1 = 13), we find the critical point, respectively:

Since the observed value of the criterion is less than the critical value (1.875<2,67), то нет оснований отвергнуть гипотезу о равенстве генеральных дисперсий. Таким образом, исправленные дисперсии различаются между собой незначимо.

The problem considered is not easy at first glance, but it is quite standard and can be solved according to a template. Such problems differ from each other, as a rule, in the values ​​of the criteria and the critical region.

More labor-intensive (as they contain a lot of calculations, some of which are summarized in tables) are tasks to test the hypothesis about the type of distribution of the population. When solving such problems, various criteria are used, for example, the Pearson criterion.

Problems of determining the type of distribution law from statistical data

This type of problem belongs to the section that studies the elements of correlation theory. If we consider the dependences of Y on X, then we could recall the least squares method to determine the type of dependence. However, in mathematical statistics everything is much more complicated and in the theory of correlation two-dimensional quantities are considered, the values ​​of which are usually given in the form of tables.

	x 1	x 1	…	x n	n y
y 1	n 11	n 21	…	n n1
y 1	n 12	n 22	…	n n2
…	…	…	…	…	…
y m	n 1m	n 2m	…	n nm
n x			…		N

Let us give the formulation of one of the tasks of this section.

Task

Determine the sample equation of the straight line of regression of Y on X. The data are given in the correlation table.

Y	X				n y
	10	20	30	40
5	1	3			4
6		2	1		3
7			3	2	5
8				1	1
n x	1	5	4	3	N=13

Conclusion

In conclusion, we note that the level of complexity of problems in mathematical statistics varies quite a lot when moving from one type to another. Problems of the first type are quite simple and do not require a special understanding of the theory; you can simply write down formulas and solve almost any problem. Problems of the second and third types are a little more complicated and to successfully solve them, a certain amount of “knowledge” in this discipline is required.

We will give a list of only two books, but these books have long become reference books for the author of this article.

1. Gmurman V.E. Probability theory and mathematical statistics: textbook. – 12th ed., revised. – M.: Publishing House Yurayt, 2010. – 479 p.
2. Gmurman V.E. A guide to solving problems in probability theory and mathematical statistics. – M.: Higher School, 2005. – 404 p.

Custom mathematical statistics solution

We wish you good luck in mastering mathematical statistics. If there are problems, please contact us. We'll be happy to help!